Belt drive¶

Belt drive link properties implement a toothed belt drive. Only the linear elastic behaviour is modelled, non-linearities are neglected. The simplifications are:

the belt is always considered prestressed (both strands are contributing to the stiffness)
the prestress force is not modelled and has to be added as load in an analysis if desired
irregular transmission due to the teeth is not modelled
local deformation of the pulleys is not modelled

Definition¶

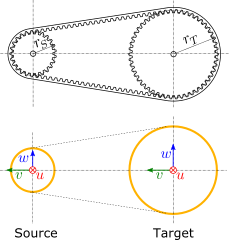
Source and target interfaces should be chosen as shown in following figure:

Source interface¶

Type	Stationary interface (6dof)
Topologies	Peripheral face of the source pulley
Location	Center of the source pulley
u direction	Axial, along the axis of rotation of the source pulley
v direction	Pointing towards the center of the target pulley
w direction	Resulting direction

Target interface¶

Type	Stationary interface (6dof)
Topologies	Peripheral face of the target pulley
Location	Center of the target pulley
u direction	Axial, along the axis of rotation of the target pulley
v direction	Aligned with the v-direction of the source interface
w direction	Parallel to the w-direction of the source interface

Recommended link settings¶

Use ground for source	unchecked
Location master	none
Orientation master	either source or target

Parameters¶

Parameter	Unit	Symbol	Description
Source gear radius	m	\(r_S\)	Radius of the pitch line of the source pulley
Target gear radius	m	\(r_T\)	Radius of the pitch line of the target pulley
Belt stiffness	N/m	\(k\)	Stiffness of one strand of the belt including tooth compliance
Belt viscous damping	Ns/m	\(d_v\)	Viscous damping coefficient of one strand of the belt
Belt hysteretic damping	None	\(d_h\)	Hysteretic damping coefficient of one strand of the belt

The stiffness of the belt can be calculated using the specific stiffness \(c_{st}\), the width of the belt \(b\), and the free lenght of a strand \(l_{1}\) according to \(k = c_{st} \, b / l_1\).