How does gravity affect the geometric errors of your machine tool? Does the impact of gravity on your manufacturing accuracy vary at different positions of the axes? If only there was a way to simulate these effects efficiently…
MORe is the perfect tool to evaluate effect of the own weight of the machine parts. Using novel simulation methods, MORe offers the possibility to evaluate the deformation of the machine tool at different axis positions. This blog post presents an interesting case study showing you how to evaluate the geometric performance of your machine tool design.
Model setup
The RMT MORe model is used. It is a 3-axis machine tool model with linear direct drives in X-, Y- and Z-direction. This is the model we use in our courses to teach you the capabilities of MORe.

Simulation of the effect of gravity
In order to evaluate the effect of the own weight, we need to define a static mechanical analysis. We consider gravity as the single mechanical load of the simulation. Additionally, we can provide the position of the axes. MORe provides a convenient interface to input the axis positions as a table. With a single button press, we can evaluate the deformation of the structure for a desired number of positions of the axes.
In the animation below, we can see the deformation of the machine tool due to gravity when moving along the Z-axis. The postprocessor, updated since MORe 3.0 Castaneda, allows you to interact conveniently with the simulation results. The figure shows the displacement between the tool center point (TCP) and the workpiece in Z-direction along the 300 mm of stroke of the Z-axis. We can observe that the higher the Z-slide the larger the displacements in Z-direction due to the own weight. This analysis allows us to estimate the positioning error of the Z-axis due to the effect of gravity, which remains around 2.5 μm.
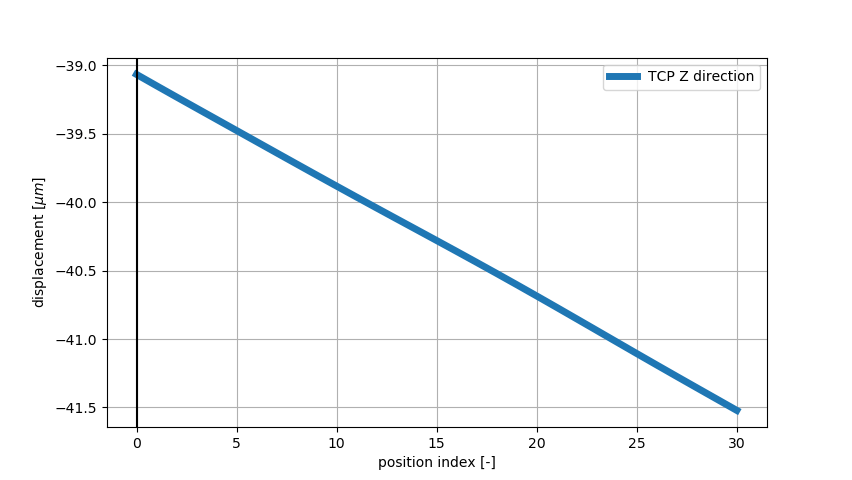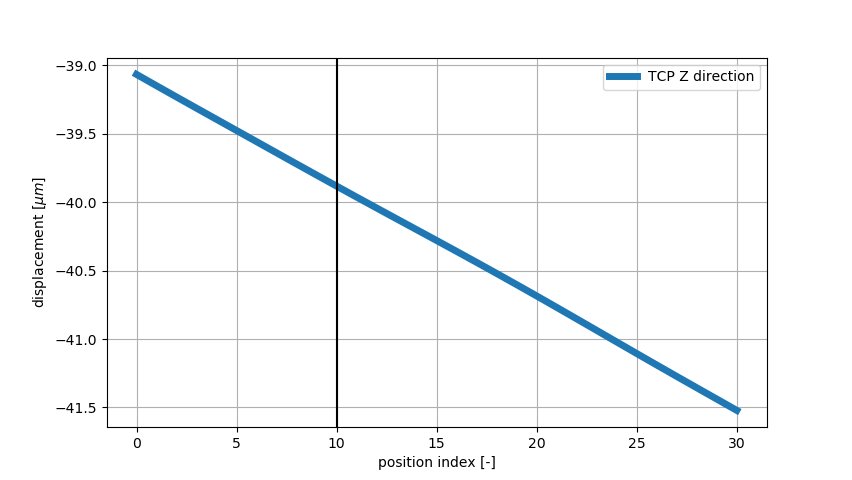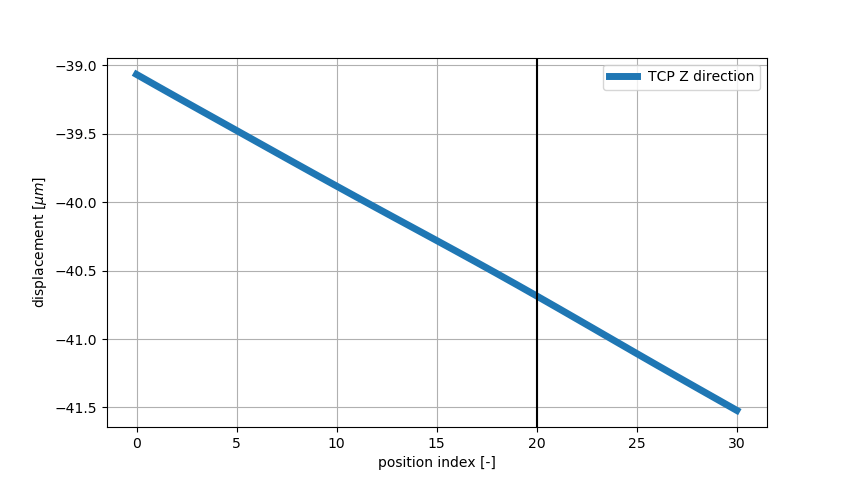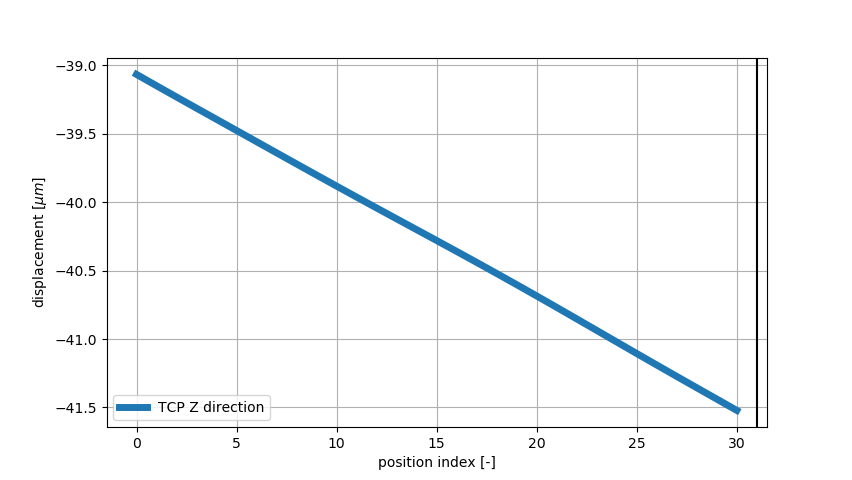

We can perform a similar study with the X-axis. We show in the figure the displacement between the TCP and workpiece in Z-direction when moving the X-axis over 500 mm. We can observe that weight of the structure results in a straightness error of the X-axis of around 0.8 μm.


Advanced postprocessing options
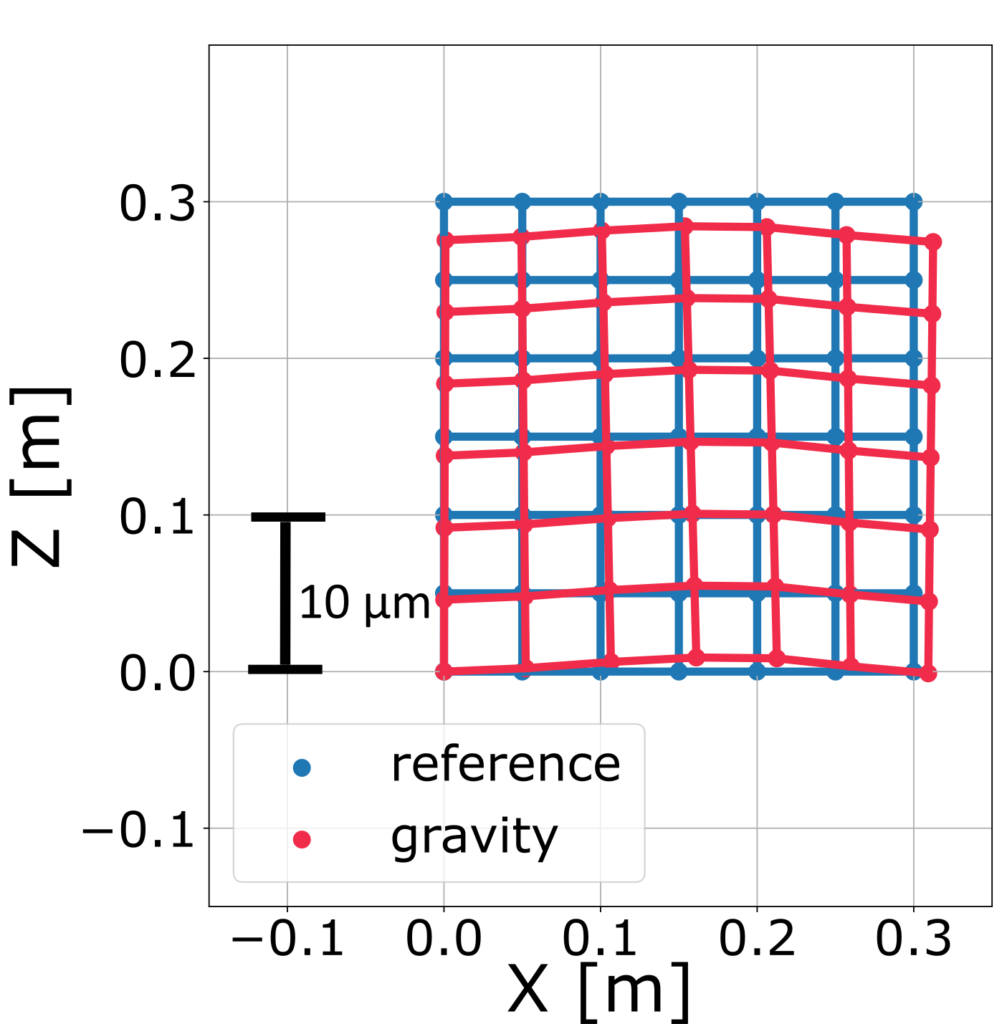
The displacements of the TCP due to gravity provide a valuable information about the geometric errors of each of the linear axes. However, it might be interesting to evaluate the TCP displacements in the whole working volume. Therefore, we can define a static mechanical analysis in MORe at several positions of linear axes. MORe provides the possibility to export the results as tabular data or as Matlab files. Furthermore, a comprehensive Python API facilitates the interaction with the results of the postprocessor with scripts. These different possibilities to interact with the simulation data enable us to visualize the deformation in the whole working volume.
We create uniform grid of 300 x 300 mm spaced 50 mm in the XZ and YZ plane. We depict in blue the reference grid and in red the deformed grid, setting the displacement of the point at the origin of the coordinate system as zero. In the figure representing the errors in the YZ plane, we can observe that the gravity affects predominantly the squareness error between the Y- and Z-axis. This angular error is around 45 µm/m and results in deviations of the TCP in negative Y-direction. Furthermore, the deformation of the column leads to a positioning error of the Z-axis. The figure depicting the errors in the XZ plane provides information about the straightness error of the X-axis due to the movement of the column.

Take-home message
In this blog post, we learnt how to use virtual prototypes to evaluate the effect of gravity on the volumetric errors of the machine tool. The errors due to the own weight are strongly dependant on the position of the axes. The weight of the parts of the machine tool have a direct impact on the geometric errors, such as squareness, positioning error, and straightness error.
Does this sound interesting to you? Check out our latest MORe release and start exploring how you can use these analyses to improve the precision of your machine tool.

